协作臂的设计出发点是模拟人的手臂 ,在某些特定场景下(人们越来越懒,越来越娇贵,苦活脏活累活都不想自己干),代替手臂进行抓取、码垛、喷漆、打磨等操作。新手小白要学习协作臂,理解各种基本概念,理所当然应该从重新认识我们的手臂开始。
想一想,手臂有几个关节?
从躯干往手掌方向,依次是肩、肘、腕关节。
• 肩关节运动范围大,大臂绕肩关节,可以进行上下、前后和扭转运动;
• 肘关节可以让大、小臂张合,大力水手秀肌肉的时候,一般都会弯曲肘关节;
• 腕关节灵活,可以拧螺丝、挪动鼠标(打CS)、拍手;
手臂灵活吧,这里其实已经涉及到自由度(DoF, Degree of Freedom)的概念。
机器人的自由度(DoF, Degree of Freedom),表示机器人位形所需的最小实值坐标数。——《现代机器人学-机构、规划和控制》
操作臂的自由度,是操作臂中具有独立位置变量的数目,这些位置变量确定了机构中所有部件的位置。——《机器人学导论》
概念不太好理解?举个两粟子:
• 家里卧室的门,自由度是1,因为只需要门与门框的夹角这一个变量就可以确定门的位置;
• 办公桌面上平放的一张A4纸,自由度是3,首先平面内用x,y确定A4纸中心的相对桌面的位置,再用一个转角确定A4纸长的边相对于桌面的角度。
机器人结构各异,这样算自由度好麻烦,没关系已经有大神推出了公式:
Kutzbach - Grubler公式
DoF = m(N-1-J) + sum_{i=1}^{J}{f_{i}}
对于一个具有N个构件(含基座)的机构,令J为关节数,m为刚体的自由度数(对于平面机构,m=3;对于空间机构,m=6),fi为关节i对应的自由度数。注意:此公式只有在所有关节约束都独立的情况下才成立,否则,只能用于判断自由度的下限值。
这下可以开算了,这回是书上的粟子,都是平面机构:
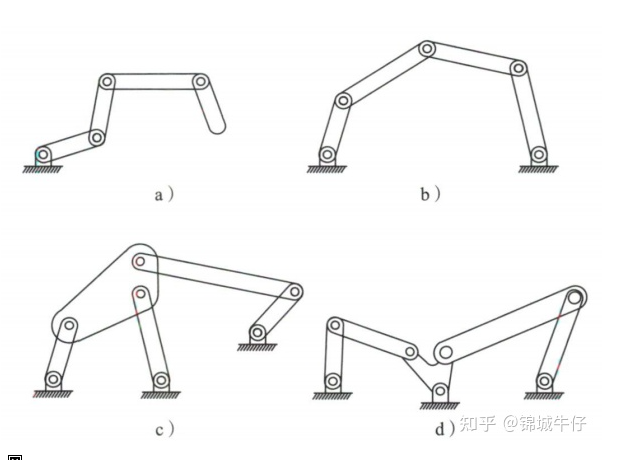
图a)机构的自由度,N=5,J=4,每个关节的自由度为1,dof = 3(5-1-4)+4 = 4
图b)机构的自由度,N=5,J=5,每个关节的自由度为1,dof = 3(5-1-5)+5 = 2
图c)机构的自由度,N=6,J=7,每个关节的自由度为1,dof = 3(6-1-7) + 7 = 1
图d)机构的自由度,N=6,J=7,每个关节的自由度为1,dof = 3(6-1-7) + 7 = 1
现在,再回看看手臂的自由度是多少,能不能套用这个公式。首先N = 4(躯干(基座)、大臂、小臂、手),J = 3(肩、肘、腕)。
再来确定一下,手臂各个关节的自由度,上图来照着说。
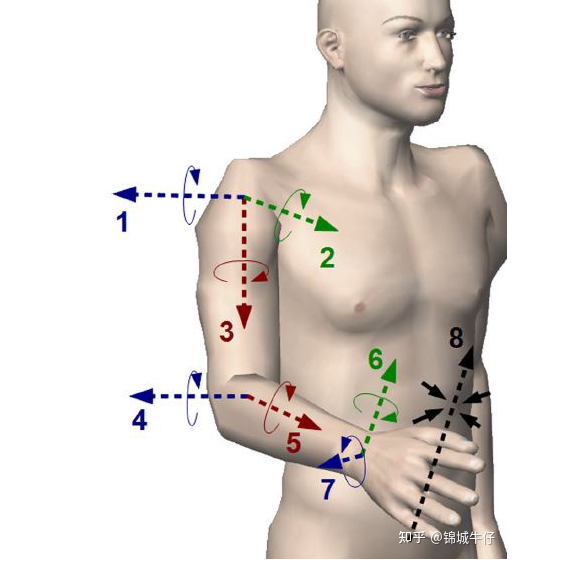
图中每个箭头代表一个自由度,解释一下:
• 肩关节,固定在躯干上,不能移动,但能转动。3个自由度:
• 1轴,肩关节前后运动;
• 2轴,肩关节左右运动;
• 3轴,肩关节带动大臂转动;
• 肘关节,连接大臂和小臂,只能弯曲,1个自由度;
• 肘、腕关节配合,由尺骨和桡骨转动,使腕关节可以转动,1个自由度(拧钥匙);
• 腕关节,本身可以本左右摆动(玩鼠标),可以上下摆动(招手),2个自由度;
套用前面的公式,手臂自由度 dof = (4 - 1 - 3) + 3(肩)+1(肘)+3(腕) = 7;
接下来看看这个图,反手摸肚脐。大部分人的手臂都做不到,这又引入了一个概念,那就是工作空间。

机械臂的工作空间,简单的说就是机械臂可以到达的所有位置的。
机械臂由于本身设计的原因,有些位置是不能到达的,用数学来解释,就是逆运动学方程无解。下图为某协作臂的工作空间,中间的圆柱形区域是不能到达的。

